点云基于图论的处理方法

点云
14 分钟 读完 (大约 2158 个字)

本系列是按照bilibili上刘永成博士的分享课的论文笔记，主要针对点云基于图论的处理方法。
这一部分主要讲解的方法包括：DGCNN、RGCNN、Spectral Graph Convolution、DeepGCNs

DGCNN (TOG 2019)

DGCNN: Dynamic Graph CNN for Learning on Point Clouds

具体思想

  • 改进pointNet方法。主要是pointNet在特征提取中只考虑各个点的特征，未对相邻点进行考虑。PointNet的主要流程是：先单独计算（更新）每个点的feature，更新多次之后，最后用global pool将所有点的feature整合为一个点云的feature。在更新每个点的feature时，只与这个点之前的feature有关，与其它点的feature无关。作者在论文中认为：每个点的feature在计算（更新）过程中彼此独立，每个都相可以看作是一个全局feature。这可能就是一个值得改进的地方。
  • 提出动态图的想法，每经过一次edgeConv之后都要重新提取一次动态图，即knn特征提取。使得特征感受野逐步增加。

核心部分

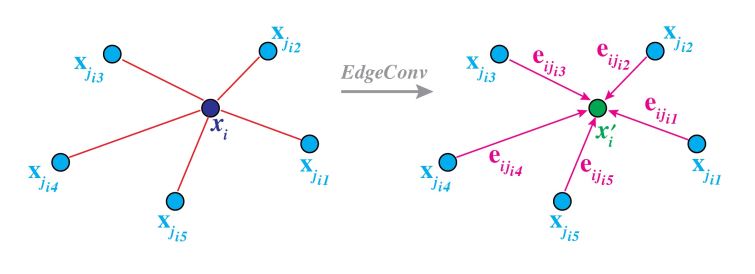
edgeConv

  • 输入特征维度为$(n,c_1)$， 针对每一个点$x_i$计算它的knn，即k个相邻点(使用top-k即升序得到)。
  • 计算每个点的edge特征：$x_{j_{i1}}-x_i,…,x_{j_{ik}}-x_i$
  • 将点的特征和边的特征连接起来。$(x_i, x_{j_{i1}}-x_i),….,(x_i, x_{j_{ik}}-x_i)$
  • 使用共享参数的全连接层来进行特征提取。代码中可以用1x1的卷积来实现。得到k个特征。
  • 用max-pool这种对称函数来提取每个点的特征。输出特征维度为$(n,c_2)$。

这样一来更新权重的时候，每一个点的权重更新不止于这个点的特征有关，还与周边的k个最邻点的特征有关。

20200214163457.png

动态图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
x = get_graph_feature(x, k=self.k)
x = self.conv1(x)
x1 = x.max(dim=-1, keepdim=False)[0]

x = get_graph_feature(x1, k=self.k)
x = self.conv2(x)
x2 = x.max(dim=-1, keepdim=False)[0]

x = get_graph_feature(x2, k=self.k)
x = self.conv3(x)
x3 = x.max(dim=-1, keepdim=False)[0]

x = get_graph_feature(x3, k=self.k)
x = self.conv4(x)
x4 = x.max(dim=-1, keepdim=False)[0]

x = torch.cat((x1, x2, x3, x4), dim=1)

在每一次edgeConv之前要进行新特征的图提取，提取出新特征每一个点的k个相邻特征。这样图结构就变成动态的，能够自适应不同数据。越深的特征感受野也就越大。如代码所示也将不同感受野的特征进行了连接操作。

Regularized GCNN. MM 2018

RGCNN: Regularized Graph CNN for Point Cloud Segmentation

具体思想

  • 用图论的思想处理点云数据，论文中graph中说的是全连接图，即点云中所有点是互通的。然后用正则化的图卷积来进行特征提取。
  • 用切比雪夫多项式拟合$L^k$降低计算复杂度。
    结构图如下所示：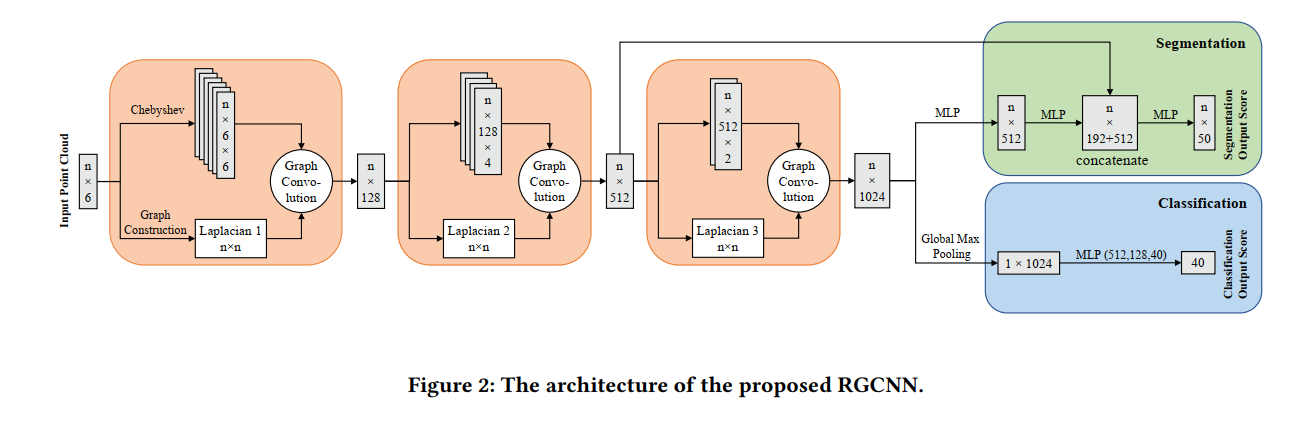
    20200216222435.png

这篇文章只讲关键部分，具体推导请看我的另外一篇GCN的博客。

核心部分

邻接矩阵A、度矩阵D、拉普拉斯矩阵L

  • A: 定义的图结构为全连接图，计算点云的A矩阵的公式为：
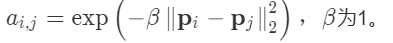
    20200217152438.png
  • D: 因为图结构是全连接，所以度矩阵D为对角线为点云总点数的对角阵。
  • L: 正常L = D - A，归一化的L为: $\boldsymbol{L}=\boldsymbol{D}^{-1 / 2}(\boldsymbol{D}-\boldsymbol{W}) \boldsymbol{D}^{-1 / 2}=\boldsymbol{I}_{n}-\boldsymbol{D}^{-1 / 2} \boldsymbol{W D}^{-1 / 2}$

图卷积

  • 因为点云所在的空间不像图像类似的欧式空间，我们可以建立点云之间的拓扑图，在这个拓扑图上进行特征提取。所以这也是另外一个处理点云数据的方法。
  • 将空域的数据转换为频域上面，用傅里叶变化进行变换计算之后再通过傅里叶逆变换转换回来。$\mathbf{x} *_{\mathcal{G}} \mathbf{y}=\mathbf{U}\left(\mathbf{U}^{T} \mathbf{x}\right) \odot\left(\mathbf{U}^{T} \mathbf{y}\right)$，其中$U^Tx$为傅里叶变换，$Ux$为逆变换，相乘方式为逐点乘。
  • 通过滤波提取有用特征:
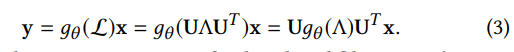
    20200216225142.png

20200216230143.png

切比雪夫多项式

使用切比雪夫截断法来拟合$L^k$降低计算复杂度。
20200216225627.png

结合代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def chebyshev5(self, x, L, Fout, K):
        # If K == 1 it is equivalent to fc layer
        N, M, Fin = x.get_shape()
        N, M, Fin = int(N), int(M), int(Fin)
        x0 = x  # N x M x Fin
        x = tf.expand_dims(x0, 0)

        def concat(x, x_):
            x_ = tf.expand_dims(x_, 0)  # 1 x M x Fin*N
            return tf.concat([x, x_], axis=0)  # K x M x Fin*N

        if K > 1:
            x1 = tf.matmul(L, x0)
            x = concat(x, x1)
        for k in range(2, K):
            x2 = 2 * tf.matmul(L, x1) - x0
            x = concat(x, x2)
            x0, x1 = x1, x2
        # K x N x M x Fin
        x = tf.transpose(x, perm=[1, 2, 3, 0])  # N x M x Fin x K
        x = tf.reshape(x, [N * M, Fin * K])  # N*M x Fin*K
        # Filter: Fin*Fout filters of order K, i.e. one filterbank per feature pair.
        W = self._weight_variable([Fin * K, Fout], regularization=False)
        x = tf.matmul(x, W)  # N*M x Fout
        return tf.reshape(x, [N, M, Fout])  # N x M x Fout

和上图是一致的，W就代表着切比雪夫多项式的系数，用这个多项式去拟合高阶方程，有点类似PCA降维。

k值代表k-hop，最多能传递几步。这就和感受野比较类似。但是相对应的k越大计算复杂度越大。

Spectral Graph Convolution (ECCV 2018)

Local Spectral Graph Convolution for Point Set Feature Learning

具体思想

仍然是针对pointNet++系列，点特征已经以独立和孤立的方式被抽象，忽略了相邻点的相对布局及其特征。这一个缺点进行改进。通过在局部图上使用谱图卷积结合新的图池化策略来克服这种限制。

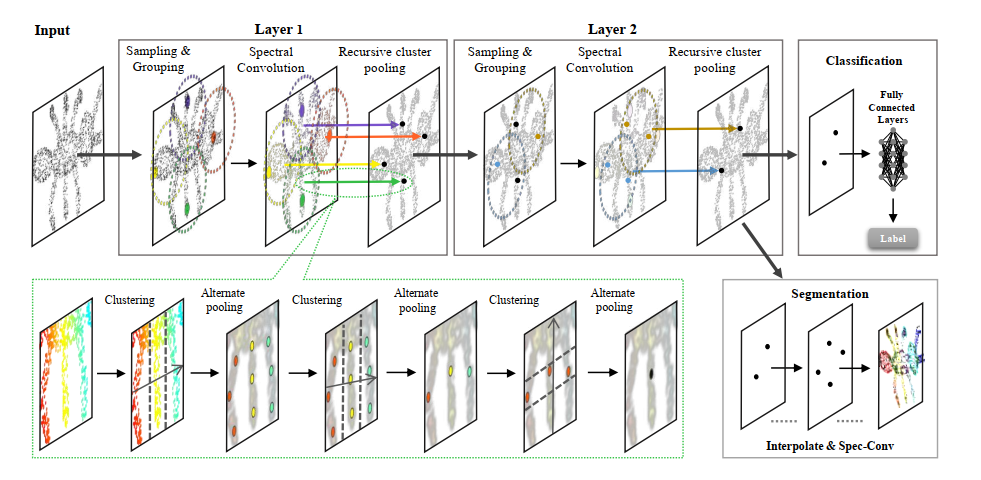
20200218151612.png

如图所示主要是三个部分：

  • 采样和knn进行分组，和pointNet++系列类似
  • Spectral Convolution，用图谱的方式提取特征，考虑了相邻点之间的联系
  • Recursive Cluster， 用谱聚类 + 交替最大池化和平均池化，来提取具有代表性的区域特征

核心部分

Spectral Convolution

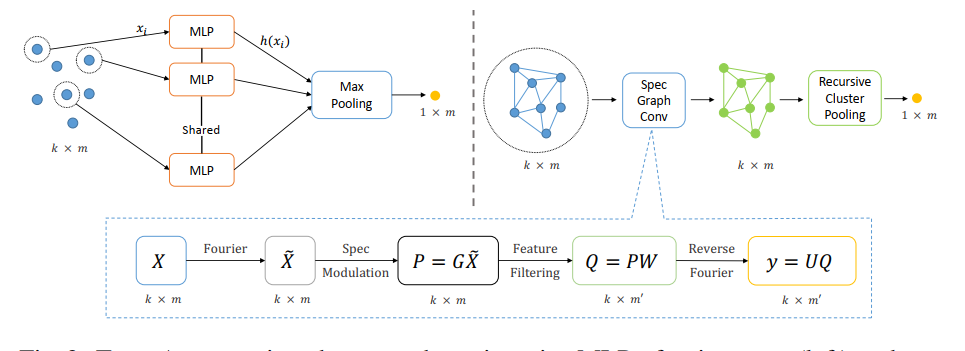
20200218152353.png

左边是pointNet++系列的方法，右边是图谱卷积的方法。
对局部点云建立图结构，用傅里叶变换和谱滤波再用傅里叶逆变换，返回空域。也是用图谱卷积提取局部点云特征的一贯方法。和上一种RGCNN不同是在局部区域中提取。

Recursive Cluster

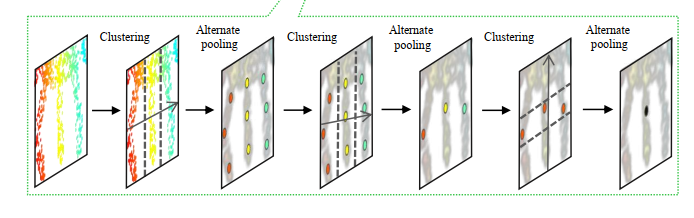
20200218152754.png

既然之前已经计算过拉普拉斯矩阵，那么当然就可以用这个来进行谱聚类。用递进的方式，逐步减少聚类中心，即cluster。结合池化操作，提取出当前区域的中心特征。

DeepGCNs (ICCV 2019)

DeepGCNs: Can GCNs Go as Deep as CNNs?

具体思想

将GCN做得跟CNN一样可以有较深的层数。GCNN因为需要聚合相邻信息，所以说有一定的平滑，导致层数不能太深。所以说作者将三个在CNN中用得比较多的方法(resnet连接方式、densenet连接方式、膨胀卷积)，用在了动态图卷积中。使得梯度不会消失，信息得以保留。

核心部分

连接方式

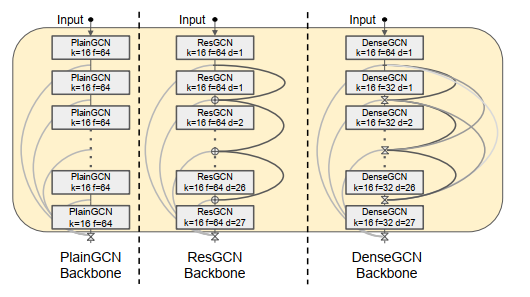
20200219193514.png

如图所示，每一层GCN都会分别提取动态图的信息，resGCN进行加和；denseGCN进行拼接。在尽可能保留信息的同时，使得层数变深，增强感受野。

图膨胀卷积

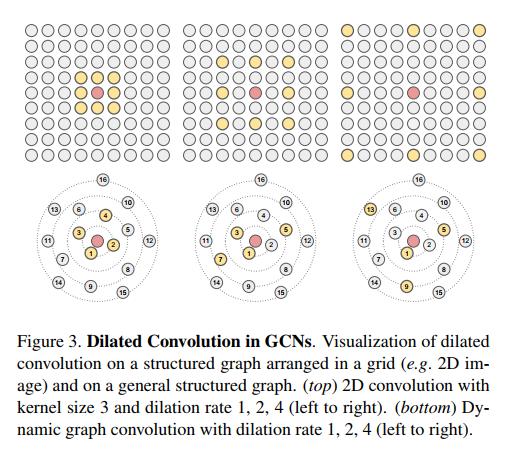
20200219193751.png

如图所示，通过knn的方式，先确定卷积区域，也即当前感受野区域。设置不同的dilation值，在不增加计算复杂度的前提下，增强感受野。和CNN中的膨胀卷积类似的效果，只是应用到图中来。

#

喜欢这篇文章？打赏一下作者吧

3D物体检测(一)
点云规则化处理(二)

评论

关注我
Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×